Deriving a Dew Point Temperature Approximation Formula
I was recently posed the following question: How do you derive the following approximation for the dew point temperature?
\[T_{dp} = \frac{4030\left( T_{db} + 235 \right)}{ 4030 - \left(T_{db} + 235 \right) \ln \phi } - 235\]Here the temperatures are in degrees Centigrade (°C) and relative humidity is a value between 0 and 1.
I had come across this formula in other contexts, but had not seen a reference or derviation of it. So I saw this as a challenge to determine the origins of this.
Not only will I present the mechanical derivation, but I’ll try to share some of the problem solving strategy that went along with it.
The first thing to notice is that the formula is a function of the dry bulb temperature and relative humidity. The dry bulb temperature is a fundamental measurement, but we do have a definition for relative humidity (\(\phi\)).
\begin{equation}\label{eq:relative_humidity} \phi = \frac{p_w}{p_{ws}} \end{equation}
Since our formula is for dew point temperature, we’ll also need the definition for that. It’s the temperature at which the associated water vapor saturation pressure is the same as the current (usually not saturated) water vapor pressure. This means:
\begin{equation}\label{eq:dew_point_temp_def} p_{ws @ T_{dp}} = p_{w} \end{equation}
We can substitute the \( p_{w} \) from Equation \eqref{eq:dew_point_temp_def} into the numerator of Equation \eqref{eq:relative_humidity}.
\begin{equation} \phi = \frac{p_{ws @ T_{dp}} }{p_{ws @ T_{db}}} \label{eq:relative_humidity_2} \end{equation}
So another way to look at the relative humidity is the ratio between the saturated water vapor pressure at the dew point temperature versus the dry bulb temperature.
At this point, we need to find the correct formulation for the water vapor saturation pressure. This is the most difficult part as it requires some intuition as to what to search for.
If you look at the Wikipedia page for ‘Vapor Pressure of Water’, you’ll see lots of different formulations. They are all approximations with varying accuracy in different temperature ranges.
To find the right approximation for this derivation, I searched for a formula that had at least one of the constants in the original formula, 4030 or 235. I was especially looking for something that had the temperature portion plus 235 (\(T + 235\)), as that is a clear pattern in the original formula.
On the Wikipedia page, the Antoine equation approximation for the saturation pressure had a \(C + T\) term where the \(C\) value was listed as being 233.426 between 1 and 99°C, and 244.485°C between 100°C and 374°C. That’s awfully close to the 235 value I was looking for. The Antoine equation has the form
\begin{equation} \log_{10} ( p_{ws} ) = A - \frac{B}{T + C} \end{equation}
This looks like the form to try. So I then started searching for ‘Antoine equation 235’ in internet searches.
I came across a paper The Use of Dew-Point Temperature in Humidity Calculations by Lawrence A. Wood, published in 1970. In that paper, in section 4, it states (this paper used \(e\) for saturation pressure):
When \(e_w\) is expressed in millimeters of mercury and \(T\) in degrees Celsius, the constants for water between 0 and 60°C have been evaluated by Dreisbach [13a, 13b] as
\(A=8.10765\),
\(B=1450.286 (°C)^{-1}\),
\(C=235.0°C\),
There’s the 235 we were looking for! Now this was a reference to other original publications. It appears the original references for these constants were:
Dreisbach, R.R. Physical Properties of Chemical Compunds, Vol. III, pg. 474 Advances in Chemistry Series No. 29. American Chemical Society, Washingtion, 1961.
Lange, N.A. Handbook of Chemistry, 10th Edition, pg. 1438. McGraw-Hill, New York, 1961.
Here’s what that actually looks like in the Physical Properties of Chemical Compunds, Vol. III reference. The constants for the Antoine equation are in the red rectangle.
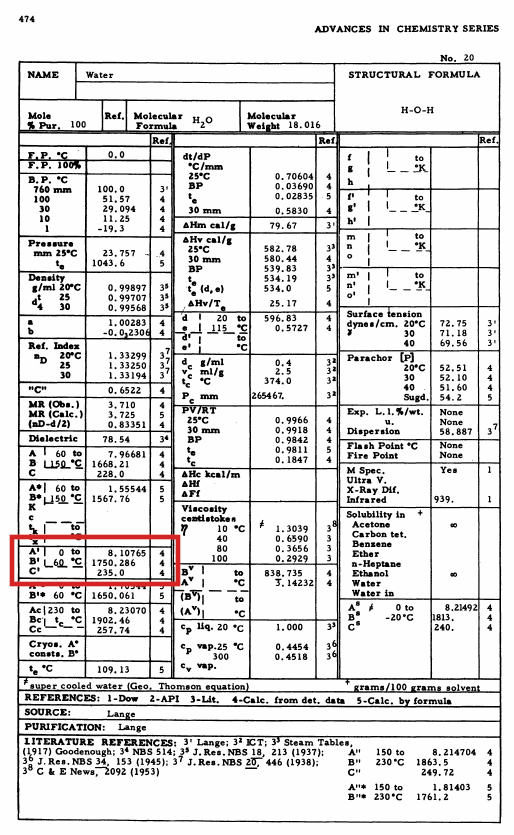
So the Antoine equation for water vapor saturation pressure that will be used to derive the original formula is
\begin{equation} \log_{10} ( p_{ws} ) = A - \frac{B}{T + C} = 8.10765 - \frac{1750.286}{T + 235.0} \end{equation}
where \(p_{ws}\) is in units of mmHg and \(T\) is in °C.
The formula for Antoine equation uses a logarithm to base 10, instead of the natural logarithm in the equations that we are trying to derive. We need to change from base 10 to base \(e\),
The change of base logarithm rule states:
\[\ln(x) = \ln(10) \log_{10} (x)\]So we can multiply both sides of the Antoine equation by \(ln(10)\) to make the left hand side change from \(log_{10} ( p_{ws} )\) to \(ln( p_{ws})\).
\[\log_{10} ( p_{ws} ) \ln(10) = \ln( p_{ws} ) = \ln(10) \left(8.10765 - \frac{1750.286}{T + 235.0}\right) = 18.67 - \frac{4030}{T+235}\]So the 4030 comes from \(ln(10)\) (which is approximately 2.3026) multiplied by the \(B\) constant 1750.286.
The Antoine equation is in a logarithm form, so the partial pressure can be explicitly solved for by exponentiating both sides.
\begin{equation} \ln( p_{ws} ) = 18.67 - \frac{4030}{T+235} \end{equation} \begin{equation} p_{ws} = e^{18.67 - \frac{4030}{T+235} } \end{equation}
Now we can substitute this into the original relative humidity formula (Equation \eqref{eq:relative_humidity_2}), and use algebra to solve for the dew point temperature and derive the original equation.
\[\phi = \frac{p_w}{p_{ws}} = \frac{p_{ws @ T_{dp}} }{p_{ws}}\] \[\phi = \frac{e^{18.67 - \frac{4030}{T_{dp}+235}}}{e^{18.67 - \frac{4030}{T_{db}+235}}}\]Using laws of exponents, and canceling \(e^{18.67}\)
\[\phi = \frac{e^{18.67 - \frac{4030}{T_{dp}+235}}}{e^{18.67 - \frac{4030}{T_{db}+235}}} = \frac{e^{18.67}e^{\frac{-4030}{T_{dp}+235}}}{e^{18.67}e^{\frac{-4030}{T_{db}+235}}} = \frac{e^{\frac{-4030}{T_{dp}+235}}}{e^{\frac{-4030}{T_{db}+235}}}\]Take natural logarithm of both sides
\[\ln(\phi) = \ln \left(\frac{e^{\frac{-4030}{T_{dp}+235}}}{e^{\frac{-4030}{T_{db}+235}}} \right)\]Using logarithm rules
\[\ln(\phi) = \ln(e^{\frac{-4030}{T_{dp}+235}}) - \ln( e^{\frac{-4030}{T_{db}+235}} ) = \frac{-4030}{T_{dp}+235} - \frac{-4030}{T_{db}+235}\]Now solve for \(T_{dp}\)
\[\ln(\phi) = \frac{-4030}{T_{dp}+235} - \frac{-4030}{T_{db}+235}\] \[\frac{-4030}{T_{dp}+235} = \ln(\phi) - \frac{4030}{T_{db}+235}\] \[T_{dp}+235 = \frac{-4030}{\ln(\phi) - \frac{4030}{T_{db}+235} }\] \[T_{dp}+235 = \frac{-4030 \left(T_{db}+235 \right) }{\ln(\phi)\left(T_{db}+235 \right) - 4030 }\] \[T_{dp}+235 = \frac{4030 \left(T_{db}+235 \right) }{ 4030 - \ln(\phi)\left(T_{db}+235 \right) }\] \[T_{dp} = \frac{4030 \left(T_{db}+235 \right) }{ 4030 - \left(T_{db}+235 \right)\ln(\phi) } - 235\]And the derivation is complete.
