A look into the shorthand formula for enthalpy
If you open up your copy of ASHRAE Fundamentals, in the chapter on psychrometrics, you’ll see a formula for the total enthalpy of moist air, \(h\), that takes dry bulb temperature, \(t\), and the specific humidity ratio, \(W\) as inputs. The complete formula, in traditional IP units (°F and BTU/lb d.a.), you will see is
\[h = 0.24 t + W \left( 1061 + 0.445 t \right)\]When I first came across this, a few question arose in my mind.
-
Where did 0.24, 0.445, and 1061 come from?
-
Why does the term related to water vapor have to have the constant, but the term for the dry air doesn’t?
Let’s first take one step back and look at the previous formula before this one. That formula, plus a few more for clarification, was
\[H_{\text{total}} = H_{\text{da}} + H_{ \text{v} }\] \[H_{\text{total}} = m_{da} h_{\text{da}} + m_{v} h_{ \text{v} }\]Divide both sides by the mass of the dry air, not total mass, and you get
\[h_{\text{total, per lb da}} = h_{\text{da}} + \frac{m_{v}}{m_{da}} h_{\text{v} } = h_{\text{da}} + W h_{\text{v} }\]I’ll have to do another post to explain why we normalize to the mass of the dry air portion only and not the total mass, but you’ll just have to take my word for now that this is a smart thing to do.
So now we can do some pattern matching and know that the \(0.24 t\) is the \(h_{da}\) and the \(W \left( 1061 + 0.445 t \right)\) term is the \(W h_{v}\) term.
Dry air portion
Under conditions that HVAC engineers will face, air can be considered as an ideal gas, and in my career, I’ve never faced a situation in which this wasn’t a good assumption. If you went through a thermodynamics course, one consequence of this is that the enthalpy is solely a function of temperature. You also should have learned that enthalpy is not an absolute property, that it requires some datum or reference. It’s analogous to potential energy, where it is the height difference that is important, not some arbitrary absolute height value.
One way to calculate a difference in enthalpy is to use the specific heat, \(c_p\). For our case, the enthalpy is just a function of temperature only, so
\[c_{p} = \frac{ \partial h }{\partial t } = \frac{ \text{d}h }{\text{d} t}\]and
\[h_2 - h_1 = \int c_p \; \text{d}t\]It would be awesome if \(c_p\) would be constant, so that this integral would just be \(c_p\) multiplied by the change in temperature. So lets check out the actual \(c_p\) values in our reference text and see what we find:
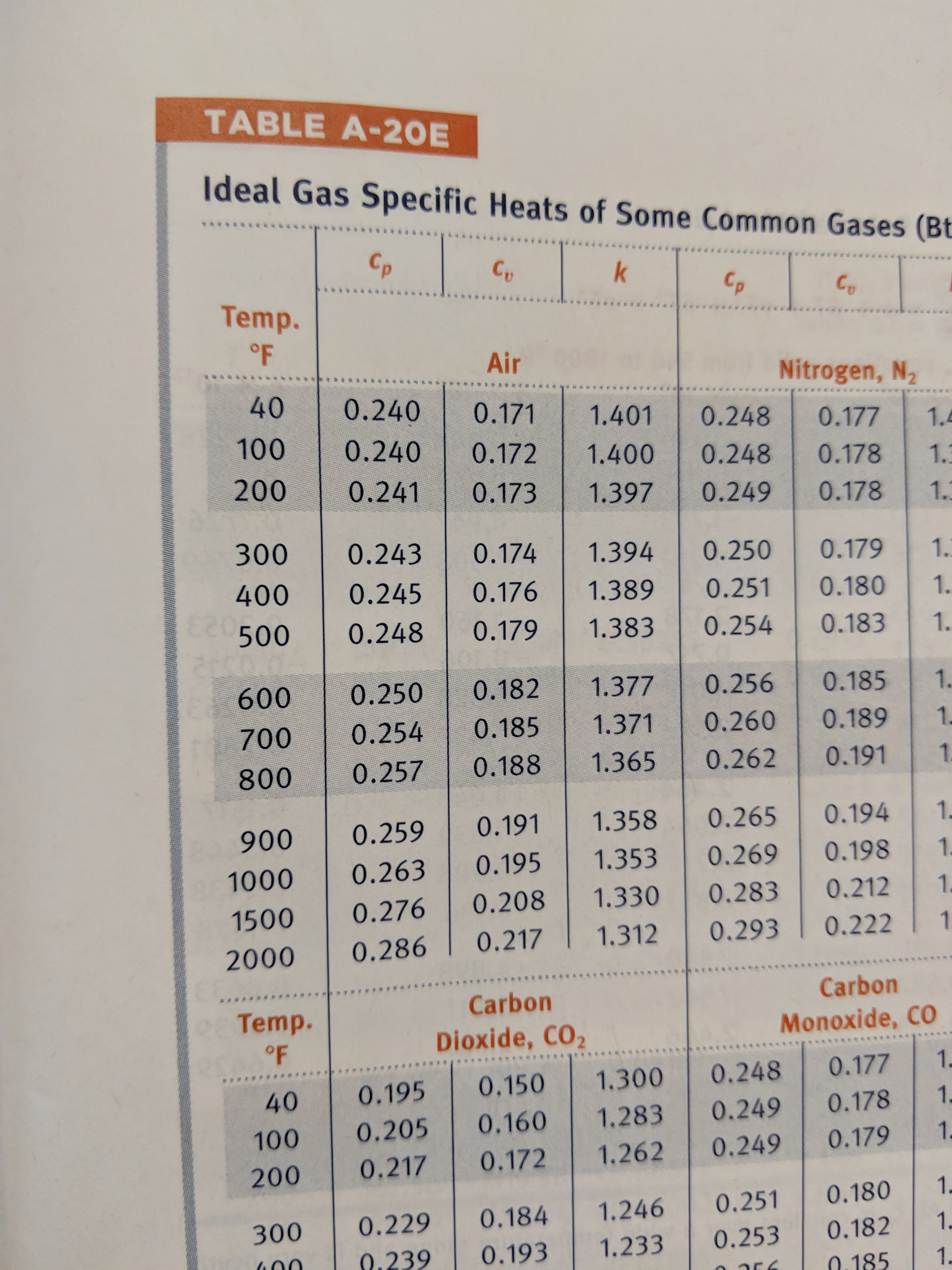
The values that we are interested in are the three in the upper left hand corner, the \(c_p\) values for air at 40, 100, and 200°F. Those values are 0.240, 0.240, and 0.241. So we are justified in taking the \(c_p\) value to be constant in the normal range of temperatures encountered in HVAC.
Cool. We also know that we can set our reference enthalpy to be whatever we’d like. So obviously, we want our calculations with dry bulb temperature in °F to be as easy as possible, so we’ll make the enthalpy 0 at 0°F, so now we have a formula for enthalpy for the dry air portion.
\[h_{da} = c_p t = 0.24 t\]Water vapor portion
Let’s now look at the \(W \left( 1061 + 0.445 t \right)\) portion.
Based on the dry air portion, it should follow that the 0.445 corresponds to the \(c_p\) value for water vapor. And from a table in my reference book, this is true.
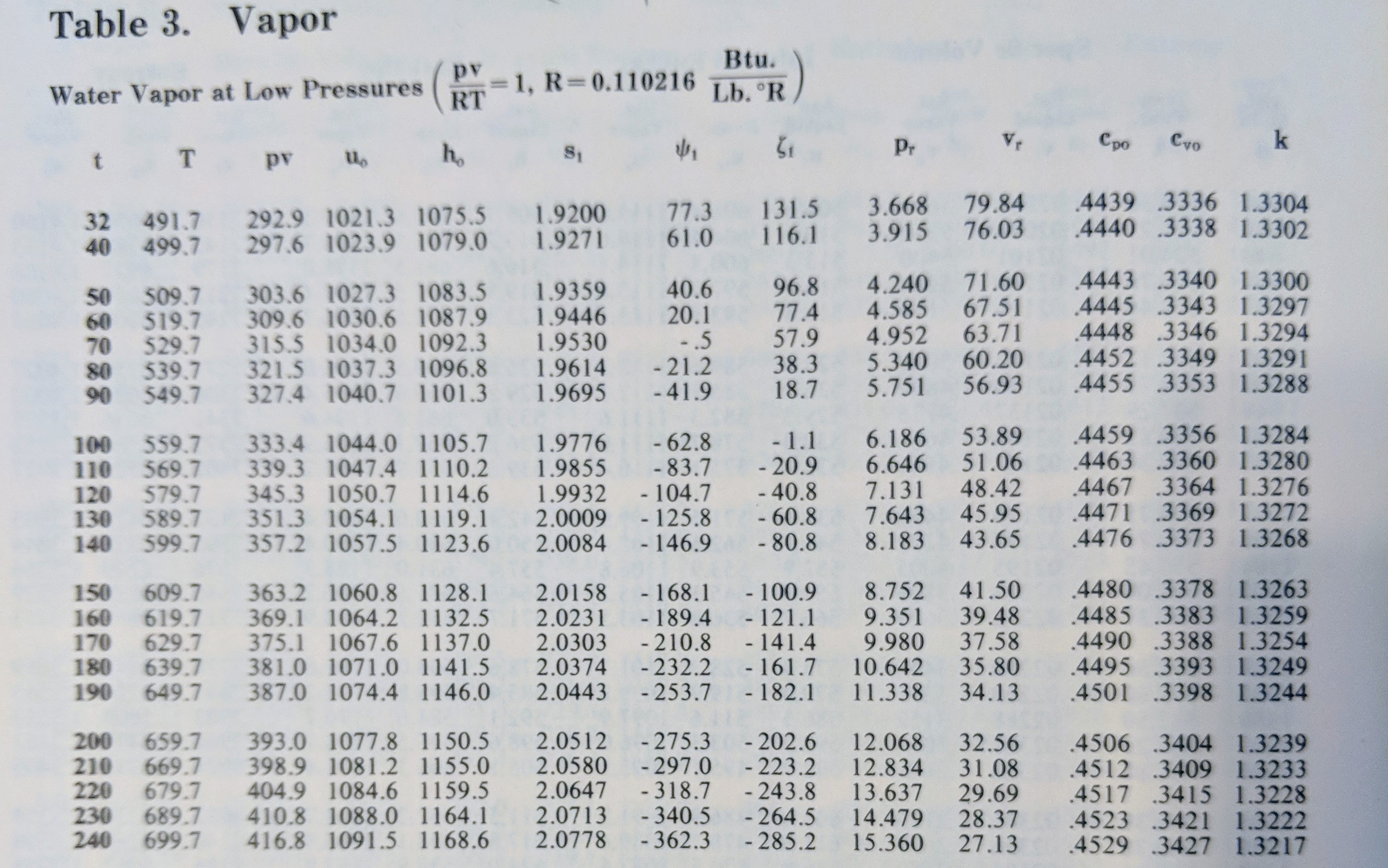
The \(c_p\) values of interest are in the third column from the right. The \(t\) values are in units of °F and the \(c_p\) values are in units of BTU/lbm-°F, so we are all good there. This table is more granular than the table I posted for air and you can see that there is more variability over the range of 32-200°F than for air, but it’s still a valid assumption to take the \(c_p\) value to be constant (it ranges from 0.4439 to 0.4506). So the authors decided that they would take a reasonable value for the corresponding temperature, and the value 0.445 was taken. This is the value for a temperature somewhere between 70-80°F, which is a pretty good value to take.
That wasn’t too hard. Now the question that bothered me after this was,
Why can’t we just do the same thing we did for air and make the enthalpy 0 at 0°F and not bring in the constant 1061 term, the formulas that are derived from this would be much simpler.
The short answer to this is that you certainly could, but you are going to quickly run into an issue when you start trying to do energy balances with real life problems.
The difference between the air portion and the water vapor portion is that for air, we are never going to have a phase change, and we are always going to be assuming it behaves as an ideal gas. But for the water portion, we normally are not going to be injecting pure, low-pressure, water vapor into air streams, but rather we are going to be taking out or putting in liquid water. This is a big difference.
Say for example, you are analyzing a cooling coil in which you are condensing liquid water out of the thermodynamic system. You will need to determine an enthalpy for that liquid water flow. How are you going to get this value? You no longer can just use the \(c_p \Delta t\) formulation because obviously liquid water isn’t an ideal gas, and you have a phase change happening.
So you will turn to your steam tables to look these values up for the liquid water or high pressure steam that no longer can be considered an ideal gas.
What reference state are those enthalpy values taken at? Well, nearly all the references I’ve come across use 32°F or 0°C of saturated liquid water to set the specific internal energy \(u\) to 0. All enthalpy values are determined from that state.
So, as a warning, if you actually come across a table that doesn’t use this as a reference state, you are going have big problems using this shorthand formula.
We are finally ready to then answer where the 1061 comes from. We want our enthalpy formula to match with the reference state given in most texts. Look at the first row of the steam table posted above for water, and check out the fifth column. The value of \(h\) in units of BTU/lbm-°F is 1075.5.
So we want a linear relationship, using our \(c_p\) from before, that makes the enthalpy value equal 1075.5 at 32°F. In mathematical form we are looking for a constant value \(C\) that makes this relationship true.
\[h = C + c_p t\]At 32°F,
\[1075.5 = C + 0.445 (32)\] \[C = 1075.5 - 0.445 (32) = 1061.3 \approx 1061\]There we have it, the 1061 appears.
Not understanding every part of this bothered me for a while, and I hope this post brings to light why these formulas were created the way they were.
